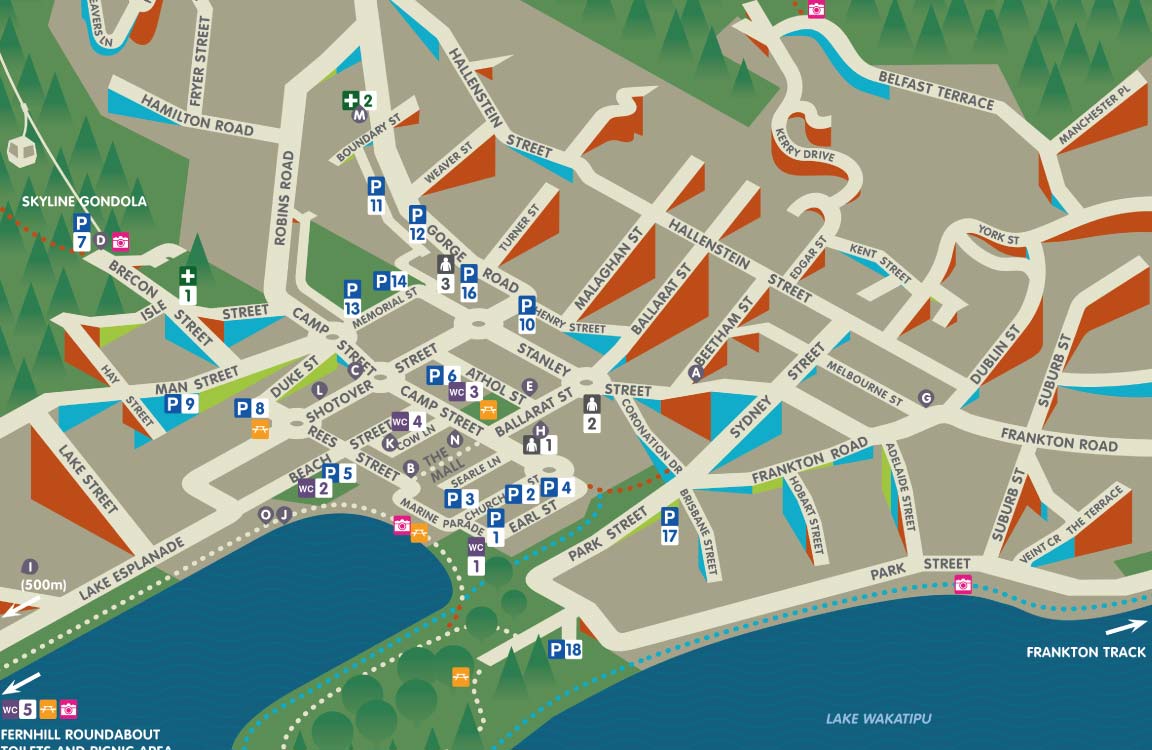
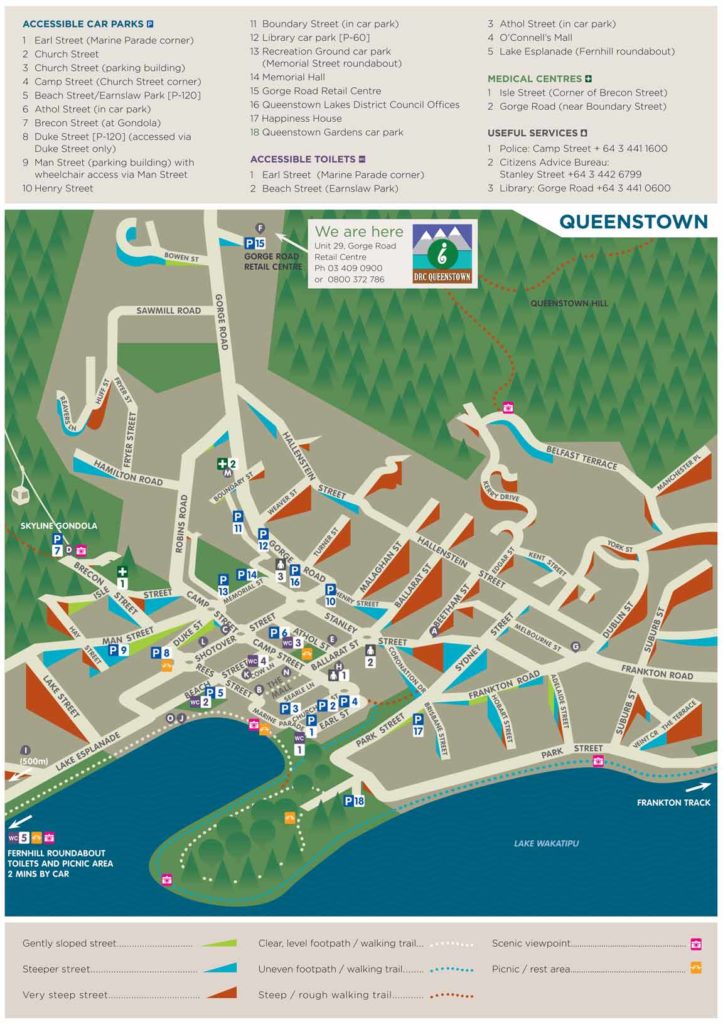
Maps solve problems. The problem here was a town with some very steep streets. People with disabilities prefer to avoid certain streets when parking or walking. How could a map design help visitors to Queenstown choose the best streets to use?
I was living in Queenstown at the time of this project. The local Disabled Resource Centre asked if I could take over a charity job for them by completing a map of Queenstown.
To be included in the map:
- A regular street map providing orientation for the town centre and lake access
- Locations of toilets and priority car parks
- An approximation of the steepness of streets for the use of people with disabilities

To begin with, The Disabled Resource centre sent me a basic plan of Queenstown with colour coded survey data overlaid. In addition to this was the beginnings of a 2D street map with a proposed method of showing steepness.

The job was printed as a two sided folding map. Advertisers had their locations marked on the map, and I got a few paying jobs on the side for those who wanted their ads designed.
This handy data and prototype map design were the start points for the map I was to make.
Up or down?
Arrows on the provided 2D street map indicated the inclines throughout Queenstown. The idea was that the direction of an arrow indicated uphill.
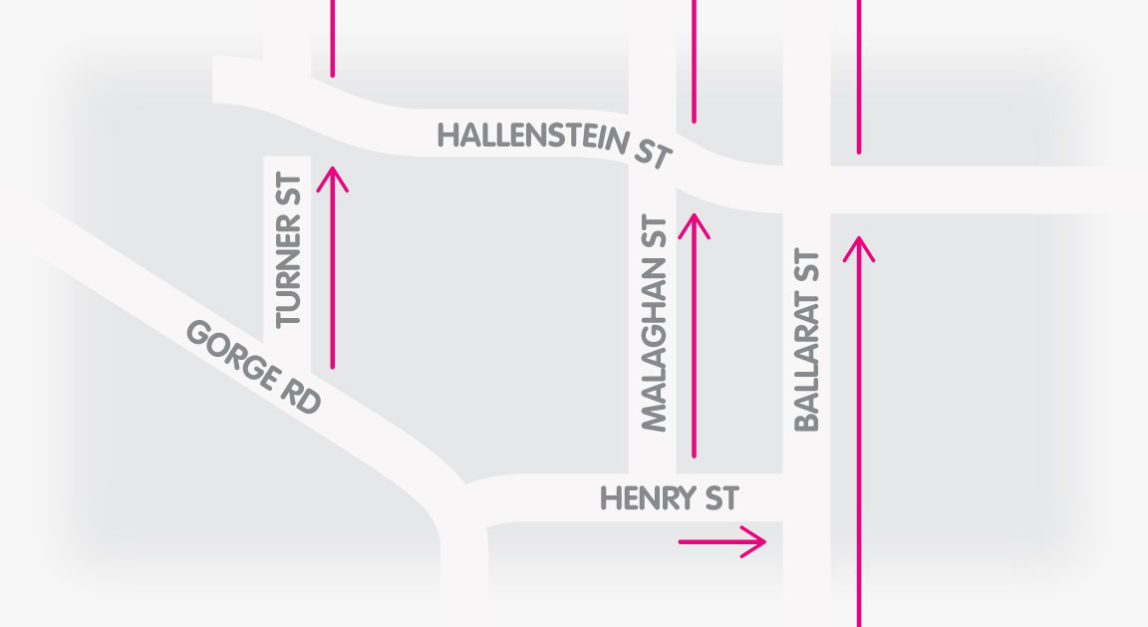
These directional arrows could be explained within the map’s key. However, I felt that this method lacked visual intuitiveness.
Wedges anyone?
Perhaps, I thought, things might work better if the arrows were long wedges instead.
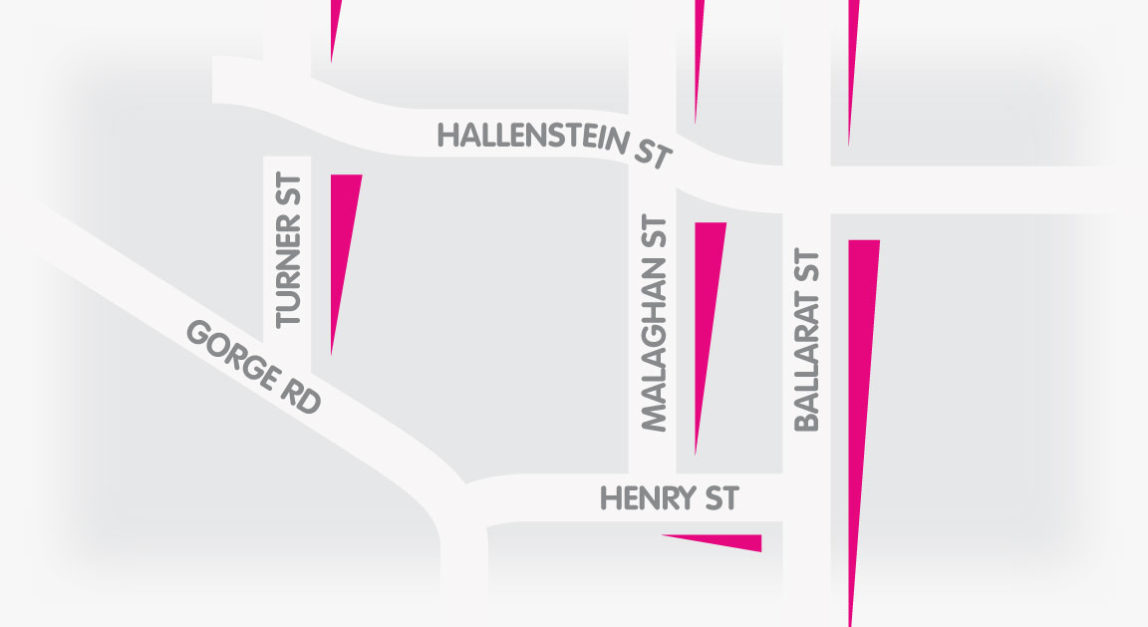
Whilst these wedges felt like an improvement, they lead me to the conclusion that I needed a vertical axis to help explain the slopes. Therefore, here was a case for a 3D map. ‘This could make an interesting design project’, I thought. At this point I had a quick ponder on how many hours the third axis would add to the project. Here was a project with no budget, but I had time. With this in mind I thought: ‘go for it’
Map design in Queenstown: What’s in an angle?
Lots of Queenstown maps have been created over the years. Many of them for tourists’ orientation. Comparatively few of these maps showed the lake at the top, or left or right.
Aside from some special reason, orienting the lake at the bottom made good sense. Consequently, the flat of the lake is in the foreground and the rising of the mountains are at the back. Due to this, and to the benefit of this particular map, the slopes of the streets are more easily depicted.
Six ways to tell if you’re projecting…
When presenting a map in 3D it’s not unusual to choose a parallel projection; thus avoiding parallel lines converging. This type of projection dates back to early Japanese and Chinese art. In those days, it was utilised to create very wide scenes on scrolls unencumbered by a vanishing point. For this reason, parallel projections quickly became common in video games many years later.
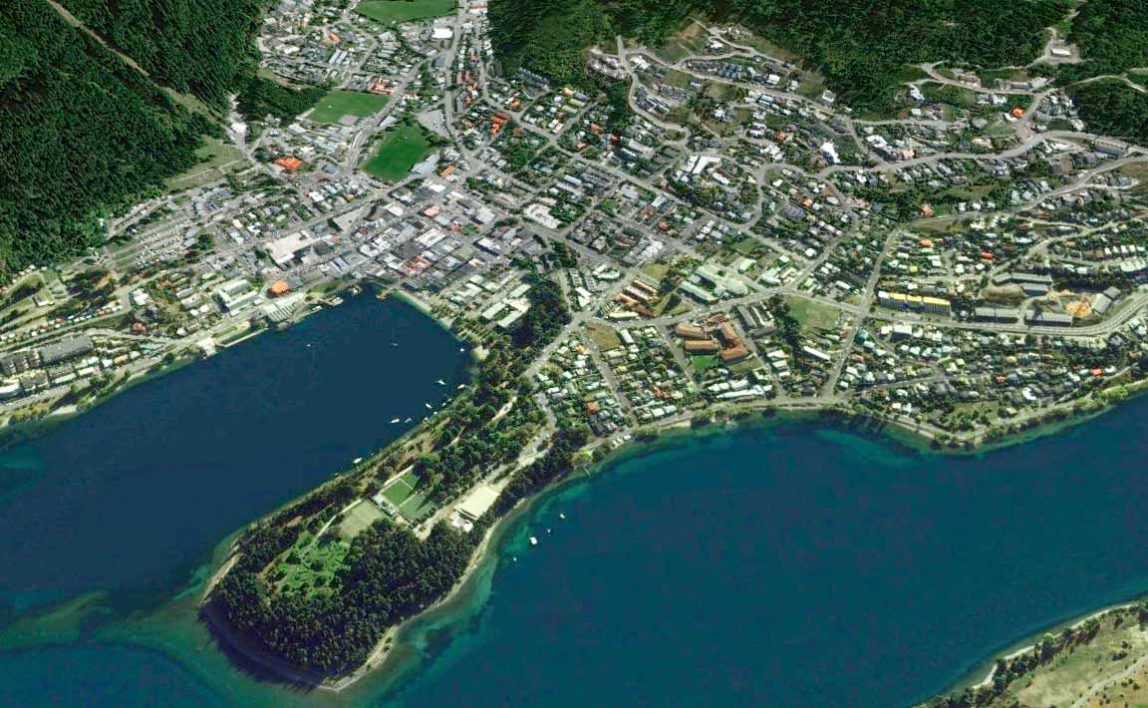
There are different types of 3D projections: ‘Cavalier’ and ‘Cabinet’ are used for furniture and architecture. They show an object’s front view flattened in plan and the sides extended diagonally upwards. ‘Military’ projection shows the top view flattened in plan and the rest of the object extended downward. Likewise, The most popular projections chosen for maps are one of the three axonometric projections. Whilst ‘isometric’ is one these projections, it’s often used to incorrectly describe the other two. With this in mind, here’s a quick look at each of the three…
Isometric
To be a true isometric projection, the three axes are spaced equally around the circle. As a result, the foreshortening along all three axes is the same. A benefit of this is that if needed, the measurements are consistent along the three axes.
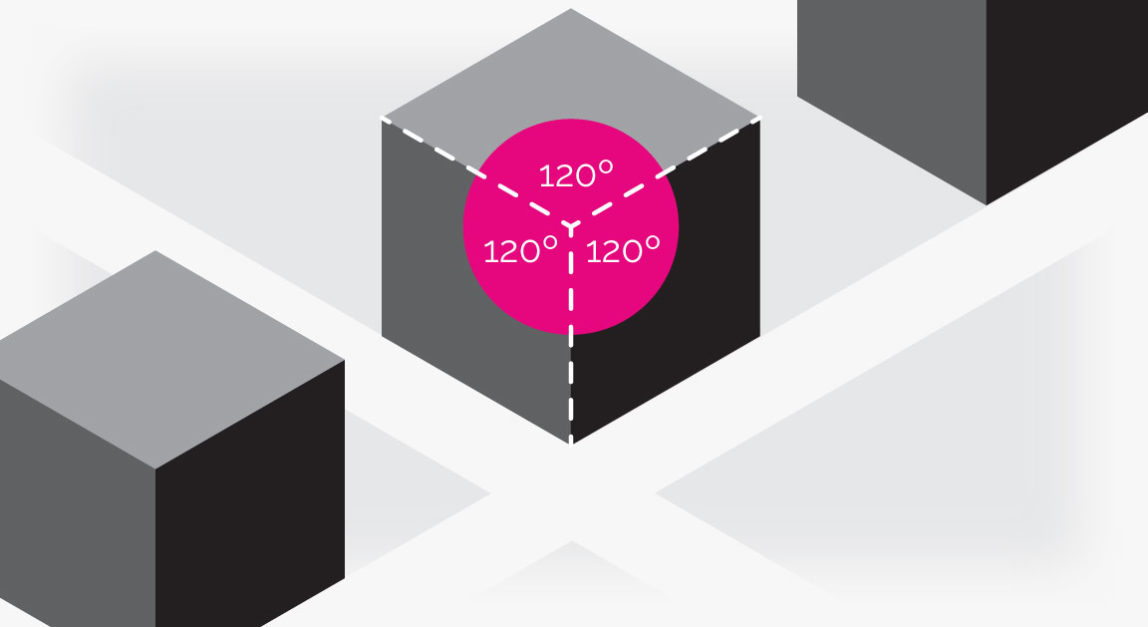
Dimetric
In a dimetric projection two of the angles are equal instead of all three. For example in the drawing below, the ground plane is tilted back to create a more natural feel. Likewise, this has decreased the angle between the two ground plane axes.
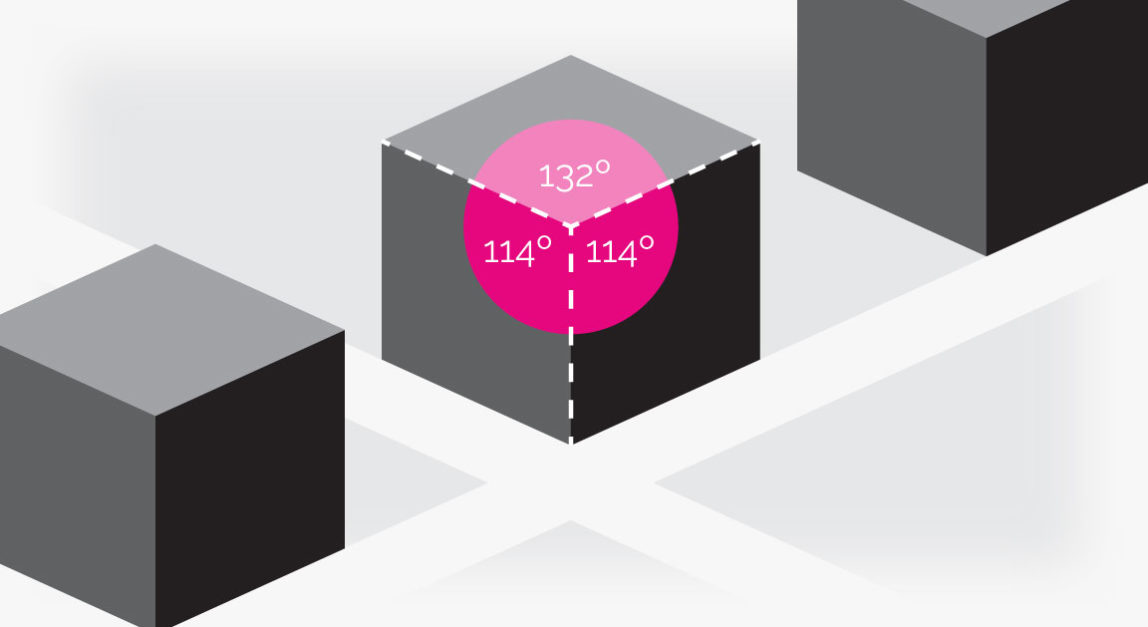
For the Queenstown and Frankton maps I chose dimetric.
Trimetric
With trimetric projection, none of the three angles are equal.
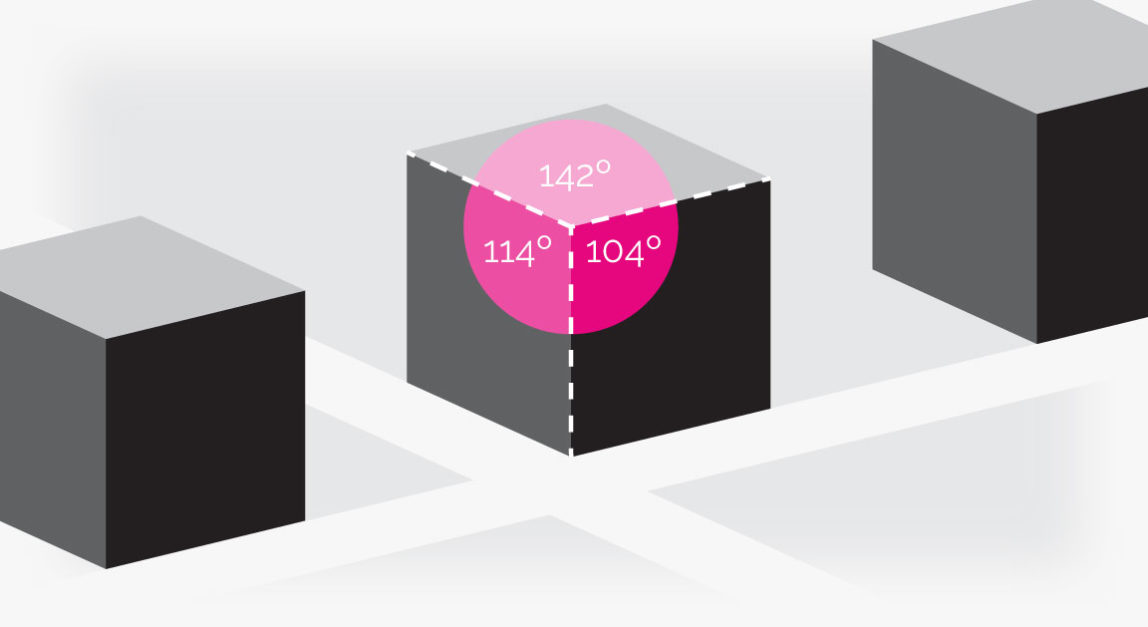
At first I used dimetric for the additional Arrowtown map design. But I later decided rotating it would better present the street plan. Therefore, I concluded there’s no one axonometric to rule them all.
The return of the wedges
The data I was supplied showed three different grades of slope. Correspondingly (and using my experience of Queenstown), I labelled the grades ‘gently sloped’, ‘steeper street’ and ‘very steep street.

After defining the slopes visually I set to work. Queenstown’s central street plan is a grid. Therefore, I started in the centre where it was easy to place this grid in dimetric angles. After that, I worked my way outwards and something pleasing started to emerge…

Frankton and Arrowtown are the other two principal centres near Queenstown. In addition to the Queenstown street plan, it was decided these two should be included on the backside of the map. Whilst the central grid of Queenstown was a useful ‘peg in the ground’ from which to grow the slopes, Arrowtown’s street plan was less uniform. It took me two attempts to get the town at a satisfactory rotation (earlier version shown below).

Frankton was more straightforward and with some cajoling I got a good angle for its terracing of streets and sloping down to the lake.
Surveying with iPad
A lack of survey data for Arrowtown or Frankton was an additional challenge. For this reason I took to the road, driving around the two towns seeking out variously inclined streets. Meanwhile, a friend in the passenger seat took readings via a spirit level app on an iPad. In addition to this, I used Google Maps Streetview to clarify some of the slopes and got a pretty good picture in the end.
The final map design
The job was printed as a two sided folding map. Advertisers had their locations marked on the map, and I got a few paying jobs on the side for those who wanted their ads designed.
Since these maps were created, The Disabled Resource Centre was disbanded due to restructuring. However, 10 years later there’s talk of a new run of them with new ads to fund it. I’m hoping this happens!

Further reading
- The Wikipedia page on 3D Projections is a great for a deeper look, and features all the projection types in one diagram.
- An incredible Japanese map, which uses two types of projection on the same map. Audaciously, it switches between them to suit its purpose. Is this unique?
- Whilst contour lines can show steepness, here’s an article about Slope Maps, which show the steepness of terrain on a 2D map using colour
- A Wikipedia page about the 1984 isometric arcade game Marble Madness with some interesting development notes.
- A roundup of tutorials for the creation of isometric (and dimetric / trimetric) objects
Share your thoughts…
Have you seen or created a map design that shows the steepness of streets? Leave a comment and share a link, or let me know what you think to this project.